Summary of Data Structures ( 1st Semester )

Single Linked List Circular

Single Linked List Circular adalah Single Linked List yang pointer selanjutnya menunjuk ke dirinya sendiri. Jika terdiri dari beberapa node, maka pointer next pada node terakhir akan menunjuk ke pointer terdepan.

          Single : artinya field pointer-nya hanya satu buah saja dan satu arah.

Circular : artinya pointer next-nya akan menunjuk ke dirinya sendiri sehingga akan membuat sebuah sirkuit atau sirkular

Ilustrasi

-         Setiap node pada linked list mempunyai field yang berisi pointer ke node berikutnya yang juga memiliki field yang berisi data

-         Pada akhir linked list, node terakhir akan menunjuk ke node terdepan sehingga linked list tersebut berputar. Node terakhir akan menunjuk lagi ke head.

Rangkaian Single Linked List tersebut diawali dengan sebuah head untuk menyimpan alamat awal dan diakhiri dengan node yang mengarah ke pointer null yang akan menunjuk ke salah satu node kembali.

Double Linked List

Pengertian Double Linked List adalah sekumpulan node data yang terurut linear atau sekuensial dengan dua buah pointer yaitu next dan prev. Dimana pointer next menunjuk ke node setelah dan node prev menunjuk ke node.

Pointer pembantu di dalam Double Linked List adalah head dan tail. Pointer ini akan digunakan dalam menunjuk elemen lain.

Ilustrasi

Pointer head akan menunjuk pada node pertama di dalam linked list dan pointer tail akan menunjuk pada node paling akhir di dalam linked list. Sebuah linked list dikatakan kosong apabila isi pointer head-nya adalah NULL. Pointer prev dari head akan selalu menunjuk NULL karena merupakan data pertama. Begitu pula dengan pointer next dari tail yang akan selalu NULL sebagai penanda data terakhir.

Beberapa operasi yang biasanya ada di dalam sebuah double linked list di antara lain :

1   1)     Push

Push merupakan operasi sebuah insert dimana di dalam linked list akan terdapat tiga jenis insert, yaitu insert melalui depan (pushDepan), insert melalui belakang (pushBelakang), ataupun insert melalui mid atau tengah dari linked list (pushTengah). Operasi pushDepan berarti data yang paling baru dimasukkan akan berada di depan data lainnya dan pushBelakang berarti sebaliknya, dimana data yang paling baru dimasukkan akan berada di belakang data lainnya.

Representasinya :

o   pushDepan : 3,6,7,10 maka hasilnya adalah 10,7,6,3

o   pushBelakang : 3,6,7,10 maka hasilnya adalah 3,6,7,10.

Push Depan

void pushHead(int age, char name[]){

     //membuat blok data baru

     current = (struct human *)malloc(sizeof human);

     //mengisi data

     strcpy(current->name, name);

     current->age=age;

     //membuat penunjuk data lain menjadi NULL terlebih dahulu

     current->next = current->prev=NULL;

     //jika tidak ada data

     if(head==NULL){

              //maka akan jadi data pertama, head dan tail akan sama dengan data baru

              head=tail=current;

     //jika ada data

     }else{

              //pergantian head menjadi data terbaru

              head->prev=current;

              current->next=head;

              head=current;

     }

}

Push Belakang

void pushTail(int age, char name[]){

     //membuat blok data baru

     current = (struct human *)malloc(sizeof human);

     //mengisi data

     strcpy(current->name, name);

     current->age = age;

     //membuat penunjuk data lain menjadi NULL terlebih dahulu

     current->prev = current->next = NULL;

     //jika tidak ada data

     if(head==NULL){

              //maka akan jadi data pertama, head dan tail akan sama dengan data baru

              head=tail=current;

     //jika ada data

     }else{

              //pergantian tail menjadi data terbaru

              current->prev = tail;

              tail->next = current;

              tail = current;

     }

}

Push Tengah

void PushMid(int age, char name[]){

     //jika tidak ada data

     if(head==NULL){

              //pushHead

              pushHead(age,name);

     //jika umur yang akan dimasukkan lebih kecil dari umur data ke head

     }else if(age < head->age){

              //pushHead

              pushHead(age,name);

     //jika umur yang akan dimasukkan lebih kecil dari umur data ke tail

     }else if(age > tail->age){

              //pushTail

              pushTail(age,name);

     }else{

              //buat blok data

              current = (struct human *)malloc(sizeof human);

              //mengisi data

              strcpy(current->name, name);

              current->age = age;

              //buat penunjuk data sebelum/sesudahnya menjadi NULL terlebih dahulu

              current->next = current->prev = NULL;

             

              struct human *temp=head;

              //mencari posisi dimana data akan dimasukkan

              while(temp!=NULL && temp->age < current->age){

                        temp=temp->next;

              }

              //memasukkan data dan menunjuk alamat-alamat data selanjutnya/sebelumnya

              current->prev=temp->prev;

              current->next=temp;

              temp->prev->next=current;

              temp->prev=current;

     }

}

22)     Pop

Pop, kebalikan dari push, merupakan operasi delete, dimana di dalam linked list memiliki dua kemungkinan delete, yaitu melalui depan (popDepan) dan melalui belakang (popBelakang). PopDepan berarti data yang akan dihapus adalah data paling belakang (akhir).

Pop Head

void popHead(){

          //jika tidak ada data

          if(head==NULL){

                   printf("No Data\n");

          //jika hanya ada 1 data

          }else if(head==tail){

                   current=head;

                   head=tail=NULL;

                   free(current);

          //jika lebih dari 1 data

          }else{

                   current=head;

                   head=head->next;

                head->prev=NULL;

                   free(current);

          }

}

          Pop Belakang

void popTail(){

          //jika tidak ada data

          if(head==NULL){

                   printf("No Data\n");

          //jika hanya ada 1 data

          }else if(head==tail){

                   current=tail;

                   head=tail=NULL;

                   free(current);

          //jika lebih dari 1 data

          }else{

                   current=tail;

                   tail=tail->prev;

                tail->next=NULL;

                   free(current);

          }

}

          Pop Tengah

void popMid(int age){

          //inisialisasi flag sebagai penanda eksistensi data

          int temu=0;

          //jika tidak ada data

          if(head==NULL){

                   printf("No Data\n");

          //jika ada data

          }else{

                   current=head;

                   //mencari posisi data

                   while(current!=NULL){

                             //pengecekan data,jika sesuai, ubah flag dan langsung break looping

                             if(current->age==age){

                                      temu=1;

                                      break;

                             }

                             current=current->next;

                   }

                   //jika data ketemu

                   if(temu==1){

                             //jika hanya data yang ditemukan adalah Head

                             if(current==head){

                                      popHead();

                             //jika hanya data yang ditemukan adalah Tail

                             }else if(current==tail){

                                      popTail();

                             //jika hanya data yang ditemukan bukan Head dan bukan Tail

                             }else{

                                      current->prev->next=current->next;

                                      current->next->prev=current->prev;

                                      free(current);

                             }

                   }else{

                             printf("Data Not Found\n");

                   }

          }

}

Circular Double Linked List

Memiliki kesamaan dengan Doubly Linked List, namun jumlah pointer di setiap node berjumlah 2 (dua) pointer.

Stack

Stack adalah kumpulan elemen data yang disimpan dalam satu laju linear. Kumpulan elemen-elemen data hanya boleh diatas pada posisi atas (top) tumpukan. Tumpukan digunakan dalam parsing, evaluation, dan backtrack. Elemen-elemen di dalam tumpukan dapat bertipe integer, real, record dalam bentuk sederhana ataupun terstruktur.

Konsep utama dari stack yaitu LIFO (Last in First Out), benda yang terakhir masuk ke dalam stack akan menjadi benda pertama yang dikeluarkan dari stack. Tumpukan atau stack mempunyai istilah pop dan push. Pop adalah penambahan elemen baru ke dalam tumpukan, sedangkan Push adalah penarikan atau penghapusan elemen yang paling atas dari tumpukan. Baik penambahan elemen maupun penghapusan elemen akan selalu dilakukan pada bagian akhir data yang selalu disebut top of stack ( karena data terakhir selalu terletak di bagian atas tumpukan ).

Terdapat beberapa operasi yang sering digunakan dalam struktur data stack. Operasi yang paling umum digunakan adalah push dan pop. Beberapa operasi yang sering digunakan yaitu :

1.     Push digunakan untuk menambah item pada tumpukan paling atas

2.     Pop digunakan untuk mengambil item pada tumpukan paling atas

3.     Clear digunakan untuk mengosongkan stack

4.     Create stack digunakan untuk membuat tumpukan baru dengan jumlah elemen kosong

5.     MakeNull digunakan untuk mengosongkan tumpukan dan menghapus semua elemen ( jika terdapat elemen)

6.     IsEmpty untuk mengecek apakah stack sudah kosong

7.     IsFull untuk mengecek apakah stack sudah penuh

Terdapat juga istilah overflow dan underflow, dimana overflow adalah keadaan dimana stack tidak bisa menampung elemen baru karena jumlah elemen sudah mencapai maksimum, sedangkan underflow adalah keadaan dimana terdapat stack kosong dan tidak ada elemen yang bisa diambil lagi.

Macam – Macam Stack

1)     Stack dengan Array

Sesuai dengan sifat stack, pengambilan ataupun penghapusan elemen dalam stack harus dimulai dari elemen teratas

2)     Double Stack dengan Array

Teknik khusus untuk menghemat pemakaian memori dalam pembuatan dua stack dengan array. Intinya adalah penggunaan hanya sebuah array untuk menampung dua stack

Queue

Queue merupan struktur data linear. Konsepnya hamper sama dengan stack, perbedaannya adalah operasi penambahan dan penghapusan pada ujung yang berbeda. Penghapusan dilakukan pada bagian depan (front), sedangkan penambahan dilakukan pada bagian belakang (rear). Elemen-elemen di dalam antrian dapat bertipe integer, real, record dalam bentuk sederhana atau terstruktur.

Queue juga disebut waiting line yaitu penambahan elemen baru dilakukan pada bagian belakang dan penghapusan elemn dilakukan pada bagian depan. Sistem pengaksesan queue menggunakan sistem FIFO (First in First Out), artinya elemen pertama yang masuk itu yang akan pertama dikeluarkan dari queue . Queue juga merupakan salah satu contoh dari double linked list.

Istilah yang dipakai apabila seseorang masuk ke dalam antrian disebut enqueue, sedangkan apabiala sesorang keluar dari antrian disebut dequeue

Beberapa operasi dalam queue :

§  Create Queue : membuat antrian baru Q, dengan jumlah elemen kosong

§  Make Null : mengosongkan antrian Q, dengan jumlah elemen kosong

§  Enqueue : berfungsi untuk memasukkan data baru ke belakang antrian

§  Dequeue : berfungsi untuk mengeluarkan data terdepan dari antrian

§  Clear : menghapus semua antrian

§  IsEmpty : memeriksa apakah barisan kosong

§  IsFull : memeriksa apakah barisan penuh

Hash Table

Hashing

Hashing adalah transformasi aritmatik sebuah string atau karakter menjadi nilai yang merepresentasikan string aslinya.           

Hashing digunakan sebagai metode untuk menyimpan data di dalam sebuah array agar penyimpanan, penambahan, dan pencarian data dapat dilakukan dengan benar.     

Hash Table

Hash table adalah table (array) dimana kita menyimpan suatu string asli, dimana index dari array adalah suatu kunci yang dienkripsi (hashed key ), namun nilainya adalah string yang asli.

Ukuran dari hash table biasanya terdiri dari berbagai macam urutan, namun biasanya lebih sedikit dari berbagai kemungkinan string. Jadi, beberapa string kemungkinan mempunyai hashed key yang sama.

Hash Function

Hashing adalah salah satu bagian penting dari data structure dimana didesain oleh suatu fungsi yang dinamakan hash function yang digunakan untuk memetakan suatu nilai dengan suatu ciri yang spesifik untuk akses elemen yang lebih cepat.

Misalkan untuk fungsi H(x) akan memetakan nilai x yang disimpan di

index x%10, maka data {11,13,15,17,19 } akan disimpan secara berturut-turut akan disimpan di index { 1,3,5,7,9 } di dalam array.

Beberapa metode untuk membuat Hash Function :

Ø Mid – Square

Ø Division

Ø Folding

Ø Digit Extraction

Ø Rotating Hash

Mid-Square

Function: h(k) = s

k  = key

s  = hash key yang diperoleh dari nilai tengah kuadrat k

·        kuadratkan string/identifier (k), lalu kita ambil angka tengah dari kuadrat string/identifier untuk dijadikan hash key (s)

Division

Function: h(z) = z mod M

z  = key

M = angka yang digunakan untuk membagi key

·        ketika ingin memunculkan index dan meletakkan key di index hasil function division

Folding

·       bagi key menjadi beberapa bagian

·       jumlahkan bagian individualnya

Digit Extraction

·       beberapa bagian digit dari key akan dijadikan hash address

·        contoh :

x = 12350. Jika kita mengambil angka ke 1, 2, dan 4, maka kita akan mendapatkan hashcode : 125.

Rotating Hash

·       gunakan metode apa saja, lalu urutan angka akan dibalik ( misalkan division atau mid-square )

·       setelah mendapatkan hash code dari hash method, lakukan rotation

·       rotation adalah dijalankan dengan menggeser digit untuk mendapatkan hash address yang baru.

·       contoh :

hash address awal = 27201

hasil rotation = 10272

Collision

·       ketika kita ingin menyimpan string menggunakan hash function sebelumnya ( menggunakan karakter pertama dari setiap string )

·       misalkan kita ingin mendeklarasikan tipe data float, exp, char, atan, ceil, acos, floor

·       maka kita akan menemukan kesamaan di tipe data float dan floor, serta tipe data char dan ceil. Ini terjadi karena kedua pasang tipe data memiliki awalan karakter yang sama, sehingga mempunyai hash key yang sama.

·       disinilah terjadi collision

Ada dua solusi umum untuk mengatasi collision :

1.   Linear Probing

mencari tempat selanjutnya yang kosong dan meletakkan string di tempat tersebut

2.   Chaining

meletakkan string sebagai linked list

Trees and Binary Tree

Tree Introduction

·        Tree adalah non-linear data structure yang merepresentasikan relasi antara objek atau data

·        Beberapa tree bisa dilihat di dalam directory structure ataupun organizational hierarchies

·        Node dari tree harus disimpan terus menerus dan bisa disimpan dimana saja, serta dihubungkan oleh pointer

Tree Concept

·        node di posisi paling atas disebut root

·        garis yang menghubungkan parent dan child disebut edge

·        node yang tidak mempunyai children disebut leaf

·        node yang mempunyai parent yang sama disebut sibling

·        degree adalah total sub tree dari sebuah node ( jumlah descendant )

·        height / depth adalah degree maksimum dari sebuah node di dalam tree

·        jika ada garis yang menghubungkan p dengan q, maka p disebut ancestor dari q, serta q disebut descendant dari p

Binary Tree Concept

·       binary tree adalah tree di dalam data structure yang mempunyai paling banyak dua children

·       kedua children tersebut biasa disebut left child dan right child

·       node yang tidak mempunyai children disebut leaf

Types of Binary Tree

·        Perfect Binary Tree adalah binary tree dengan level yang berjumlah sama dengan height/depth

·        Complete Binary Tree adalah binary tree dengan level yang berjumlah sama dengan height/depth, namun hampir terisi sempurna

·        Skewed Binary Tree adalah binary tree yang setiap nodenya mempunyai paling banyak satu child

·        Balanced Binary Tree adalah binary tree dimana tidak ada leaf yang garisnya lebih Panjang dari leaf lainnya

Property of Binary Tree

 maksimum jumlah node dari level k adalah

·        beberapa sumber menyebutkan bahwa level dari binary tree dimulai dari 1 (root)

·       height dari sebuah tree adalah total dari level diluar dari root

·       gambar di atas memiliki height sebanyak 3 ( dimana level 0 tidak dihitung karena mengandung root )

·     height minimum dari binary tree dengan n node adalah

·       height maksimum dari binary tree dengan n node adalah n-1

Binary Search Tree

Binary Search Tree adalah salah satu bentuk data structure yang mendukung searching secara lebih cepat, sorting lebih cepat, dan mempermudah insertion dan deletion.

Binary Search Tree juga dikenal sebagai versi sorting dari Binary Tree

Untuk node x = 8

• Elemen di sebelah kiri dari node x harus bernilai lebih kecil dari x
• Elemen di sebelah kanan dari node x harus bernilai lebih besar dari x

( dengan asumsi dimana setiap elemen / node bernilai berbeda satu dengan yang lain )

Basic Operation

• find(x) : find the key x
• insert(x) : insert new key x
• remove(x) : remove key x 

Search

• karena kelebihan BST dimana searching sangat mudah dengan menggunakan BST
• misalkan kita ingin mencari x
• kita akan mulai dari root
• jika di root ditemukan nilai x ( root = x ), maka search akan dihentikan
• jika nilai x lebih kecil dari root, maka pencarian akan dilakukan secara rekursif di sub tree kiri dari root. 
• Jika nilai x lebih besar dari roor, maka pencarian akan dilakukan secara rekursif di sub tree kanan dari root. 

Insertion

• Insertion dilakukan secara rekursif
• Misalkan new key adalah x
• dimulai dari root
• Jika nilai x lebih kecil dari new key, maka nilai x akan dimasukkan ke daerah sub tree sebelah kiri.
• Jika nilai x lebih besar dari new key, maka nilai x akan dimasukkan ke daerah sub tree sebelah kanan.
• Dilakukan secara rekursif sampai terdapat node kosong untuk meletakkan (dimana x akan selalu menjadi new leaf )

Berikut adalah contoh insertion dimana merupakan pencarian tempat untuk node key baru.

            

                                             

Deletion 

Terdapat tiga kondisi yang perlu dipertimbangkan : 

1. Jika key adalah leaf, maka node tersebut akan dihapus
2. Jika key adalah node yang mempunyai satu child, maka node tersebut dihapus dan child akan dihubungkan dengan parent-nya
3. Jika key adalah node yang mempunyai dua children, maka temukan 

Berikut adalah contoh deletion yang merupakan penghapusan node key.

AVL Tree adalah Binary Tree yang sudah dapat melakukan self-balancing terhadap node di dalam tree-nya

Dalam AVL Tree, terdapat 3 komponen utama yaitu:

1. Key / Data yang bersifat unik
2. Level ( perhitungan dari root sampai node / leaf terjauh )
3. Balance Factor ( perbedaan level dari anak kiri dan anak kanan )

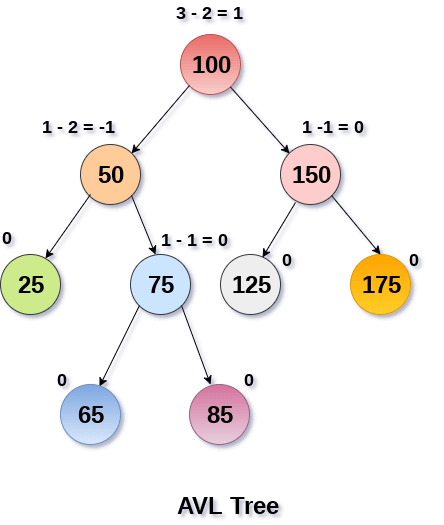
Dalam Gambar, yang diberi warna biru muda memiliki:

1. Key = 75
2. Level = 3 ( dihitung dari key 100, key 50, dan key 75 )
3. Balance Factor = 0, yang dilihat dari level anak kiri 75 yaitu, 65 dan anak kanan 75 yaitu, 85, maka 1-1 = 0

Balance Factor dapat dilihat sebagai berikut : 

• Leaves selalu memiliki balance factor 0 dan level 1 karena leaves adalah node terujung dan tidak memiliki anak 
• Dari leaves ke induknya, maka balance factor dan level dihitung dengan ketentuan: 
• Level Induk = [Level tertinggi anak] + 1
• Balance Factor = [Level anak kiri] - [Level anak kanan]
• Sebuah node tidak boleh memiliki Balance Factor lebih dari 1. Jika terdapat node yang memiliki node lebih dari 1, maka dianggap terjadi violation di dalam node tersebut. 

Insertion

Secara umum, Insertion di dalam AVL Tree sama dengan BST yaitu node dengan key yang lebih kecil akan disimpan di sebelah kiri, dan node dengan key yang lebih besar akan disimpan di sebelah kanan induknya.

Dalam gambar diperhatikan node 75 ada di sebelah kanan node 50 karena node 75 bernilai lebih besar dibandingkan node induk 50, sedangkan node 65 ada di sebelah kiri node 75 karena node 65 bernilai lebih kecil dibandingkan node induk 75.

Karena ini adalah Balanced Binary Search Tree, maka perbedaan muncul setelah insert dilakukan. Dalam AVL Tree, terdapat self-balancing yang dilakukan dengan cara mencari node yang terkena Violation

Violation dalam AVL Tree terjadi ketika sebuah node memiliki Balance Factor lebih dari 1 

Dalam Original AVL Tree, jika angka 4 diinsert, maka node 3 akan mengalami violation. Hal ini dikarenakan node akan memiliki level dan balance factor sebagai berikut :

Pada Original AVL Tree :

1.     Node 5, 9, dan 15 memiliki level 1 dan balance factor 0, hal ini karena node tersebut adalah leaf / terletak di ujung

2.       Node 14 adalah induk node 9 dan node 18, maka level node 14 adalah 3 ( dihitung level 1 dari node 14) dengan balance factor ( 1 – 2 ) = -1. Dan begitu seterusnya.

3.       Dalam simulasi point minus (-) diabaikan tetapi di dalam kode digunakan karena minus  hanya menandakan tidak seimbang ke kiri dan plus tidak seimbang ke kanan

Kita harus mempunyai persepsi bahwa :

1.       Node 4 (Child), node yang diinsert

2.       Node 5 (Parent), adalah induk dari node yang diinsert

3.       Node 3 (Grand Parent), adalah Induk dari Induk node yang diinsert

Jika node 4 di insert, maka akan terlihat seperti gambar di bawah ini :

1.       Node 4 akan masuk di sebealh kiri node 7 dan menjadi anak kiri node 5 karena node 4 memiliki key yang lebih kecil dari node 7, lebih besar dari node 3 dan lebih kecil dari node 5

2.       Setelah sampai pada posisinya, maka akan dihitung level dan balance factor dari node yang baru di insert (node 4).

Dimana :

o   Node 4 akan diberikan 1,0 karena merupakan node leaves

o   Lalu, penghitungan akan berlanjut ke induk dari node 4 yaitu 5, dengan level 2 (node itu sendiri + 1 tingkat dibawahnya) dan balance factor 1 (anak kiri = 1 (node 4) dan anak kanan = 0)

o   Penghitungan untuk induk node 5, yaitu node 3 dengan level 3 (nodenya sendiri + ada dua tingkat dibawahnya) dan balance factor 2 ( jarak terpanjang ke node leaves ), maka disini terjadi violation

Lalu, kita harus mengidentifikasi jenis Violation yang terjadi, terlebih dahulu ada empat jenis violation yang dapat terjadi :

1. Left-left case, dimana Child adalah anak kiri Parent dan Parent adalah anak kiri Grand-Parent
   
2. Right-right case, dimana Child adalah anak kanan Parent dan Parent adalah anak kanan Grand-Parent
   
3. Left-right case, dimana Child adalah anak kanan Parent dan Parent adalah anak kiri Grand Parent
   
4. Right-left case, dimana Child adalah anak kiri Parent dan Parent adalah anak kanan Grand-Parent
   

Note : H+1 menandakan adanya perubahan height (level) karena adanya penambahan node baru

Jika terjadi violation maka akan dilakukan solving/rebalancing dengan cara berikut :

1)      Jika menemukan case 1 atau case 2, maka akan dilakukan single rotation

2)      Jika menemukan case 3 atau case 4, maka akan dilakukan double rotation

Single Rotation

Terdapat dua jenis Single Rotation yaitu :

1. Left-left rotation untuk menyelesaikan case 1
2. Right-right rotation untuk menyelesaikan case 2

a.      Perhatikan bahwa S adalah induk dari SubTree A, sehingga S adalah Parent dan T adalah Grand Parent.

Note : Subtree A adalah subtree yang didalamanya terdapat node yang baru diinsert

b.      Left-left rotation dilakukan dengan putaran ke kanan dengan S berperan sebagai poros.

c.      T (Grand Parent) akan turun menjadi Right Child dari S.

d.      Subtree A akan berposisi sejajar dengan T sebagai Parent dengan status sebagai Left Child dari S.

e.      Perhatikan bahwa sebelumnya S memiliki Right Child yaitu SubTree B, sedangkan T memiliki Right Child yaitu SubTree C. Setelah left-left rotation, maka SubTree B secara otomatis akan menjadi Left Child T dan SubTree C akan tetap menjadi Right Child dari T.

f.    Kita tidak perlu mengetahui apa yang ada di dalam SubTree A,B, dan C karena yang perlu dilihat adalah pivot S,T, dan Induk dari SubTree A ( terdapat node yang baru diinsert )

Maksud dari point f, apabila node yang baru diinsert adalah node 12 (seperti gambar di samping), maka yang terlihat adalah :

1.       Node 22 berperan sebagai pivot S.

2.       Node 30 berperan sebagai pivot T, Grand Parent yang akan turun menjadi Right Child dari S.

3.       Node 15 akan berperan sebagai induk dari SubTree A ( karena mengandung node yang baru diinsert, yaitu 12 )

4.       Node 27 akan berperan sebagai induk dari SubTree B

5.       Node 45 akan berperan sebagai induk dari SubTree C

a.       S adalah Induk dari SubTree A, sehingga S adalah Parent, dan T adalah Grand Parent.

Note: Subtree A adalah sebuah subtree yang didalamnya diinsert node baru.

b.       RR Rotation dilakukan dengan melakuan putaran ke arah kiri, dengan poros S.

c.       T (Grand Parent) akan turun menjadi Left Child dari S.

d.       SubTree A naik ke tempat parent dengan mempertahankan status sebagai anak kanan S.

e.       anak kiri dari S (SubTree B) akan menjadi anak kanan dari T. Sehingga T akan memiliki anak kiri SubTree C dan anak kanan Subtree B.

f.        Kita tidak perlu mengetahui apa yang ada di dalam SubTree A,B, dan C karena yang perlu dilihat adalah pivot S,T, dan Induk dari SubTree A (terdapat node yang baru diinsert)

Double Rotation

Adalah rotasi dengan menggunakan dua metode single rotation. Jenis rotasi ini dilakukan untuk menyelesaikan case 3 dan case 4

a)       Penyelesaian dimulai dari Parent (Node S) yang akan mengakibatkan First Rotation

Untuk case 3 ini, kita diharapkan melihat child dari pivot R, yaitu anak kiri (SubTree B1) dan anak kanan (SubTree B2)

Hal yang perlu diperhatikan :

1.       Node S adalah Grand Parent

2.       Node R adalah Parent

3.       Pilih Subtree yang akan diamati.

(Dalam hal ini kita akan memilih B2 agar tidak menjadi double rotation lagi)

4.       Lakukan RR Rotation

Hasil First Rotation :

b)       Lalu, selesaikan case dari Grand Parent (node T) dan lakukan Second Rotation

Dari hasil first rotation, dapat dilihat bahwa case mirip dengan case 1, yaitu left-left case, maka akan dilakukan rotasi ke kanan dan mendapatkan hasil sebagai berikut :

Perhatikan bahwa parent R akan menjadi induk dari child S dan Grand Parent T. Hal ini akan membuat tree menjadi seimbang karena SubTree B2 yang awalnya menjadi Right Child dari R berpindah menjadi Left Child dari pivot T.

Deletion

Dalam melakukan delete node, kita harus meng-update balance factor dari masing-masing node 

untuk mengetahui apakah akan terjadi violation setelah delete.

Ketika kita melakukan deletion pada node 5, bisa dipastikan bahwa akan terjadi violation pada node 10 karena node 10 akan memiliki balance factor -2 (tidak seimbang ke kiri)

Perbaikan setelah violation seperti gambar di bawah : 

Cara mendeteksi violation adalah dengan melihat balace factor dari node dan childnya. Apabila balance factor minus, berarti kita harus cek ke bagian kanan (tidak seimbang ke kiri) dan sebaliknya. Jika seimbang, boleh pilih salah satu.

Heap

Heap adalah struktur data yang berbentuk pohon yang merupakan jenis dari binary tree. Heap juga mempunyai karakter dimana masing-masing node mempunyai maksimum dua children sebagaimana terdapat di dalam binary tree. Heap juga merupakan complete binary tree yang memenuhi sifat - sifat heap.

Heap Property

• Min Heap
• dimana setiap key dalam node bernilai lebih kecil dari children-nya

• Max Heap
• dimana setiap key dalam node bernilai lebih besar dari children-nya

Min Heap

1. Setiap key dalam node bernilai lebih kecil dari key children-nya.
2. Key yang bernilai paling kecil berada di root.
3. Key yang bernilai paling besar berada di salah satu dari node leaves.
4. Heap bisa diimplementasikan menggunakan linked list, namun lebih mudah diimplementasikan dengan menggunakan array

Applications of Heaps

• Heap Sort
• Selection Algorithm
• Graph Algorithm

Selection Algorithm

1. menemukan key minimum atau maksimum, mencari median, dan menentukan elemen k terbesar, dan lainnya
2. algoritma Djikstra, dimana digunakan untuk menemukan path terpendek dalam suatu graf
3. algoritma Prim, dimana digunakan untuk mencari minimum spanning tree (untuk mendapatkan cost terkecil)

Heap Sort

Heap sort adalah sebuah metode sorting (pengurutan) angka pada sebuah array dengan cara yang menyerupai binary tree, yaitu dengan cara memvisualisasikan array di dalam binary tree dimana index-nya akan diurutkan selanjutnya. Pada heap sort terdapat tiga bagian yaitu, node, edge, dan leaf dimana node itu adalah setiap index yang ada di dalam array, edge adalah garis yang menghubungkan dua node, dan leaf adalah setiap node yang tidak memiliki child node (node turunan). Selain itu juga terdapat root yang merupakan node awal dalam sebuah heap.

Pada metode heap sort, jenis heap tree yang digunakan adalah Max-Heap. Untuk memvisualisasikan sebuah array menjadi sebuah heap tree, maka kita harus mencari node root terlebih dahulu, dimana node root adalah node pertama di dalam sebuah tree dengan index 0. Setelah node root ditemukan, maka kita harus mencari child node dari node root tersebut. Child node sendiri terbagi menjadi dua yaitu, left child dan right child. Untuk mencari child node, kita dapat menggunakan rumus berikut :

• Left Child : 2i 

• Right Child : 2i + 1

• Parent : i/2

dimana i adalah index node yang diketahui. Jadi, apabila kita ingin mencari left child dari node di posisi pertama, maka left child-nya berada di i*2 = 1*2 = posisi kedua (index = 1, karena index dimulai dari 0), sedangkan untuk mencari right child node posisi keempat, maka right chid-nya berada di (i*2) + 1 = (4*2) + 1 = 8+1 = posisi 9 (index = 8). Untuk mencari parent dari node di posisi kelima, maka parent berada di i/2 = 5/2 = 2.5 =  posisi kedua (pembulatan ke bawah, index  = 1)

Disini kita akan memisalkan sebuah array A = 4, 1, 3, 2, 16, 9, 10, 14, 8, 7. Untuk memvisualisasikan array tersebut di dalam heap tree, kita hanya perlu menyusunnya susai dengan index masing-masing elemen.

Disini kita harus menyusun heap tree dengan function yang mengkaitkan satu elemen dengan elemen lainnya sebagai berikut :

Dengan penyusunan seperti di atas, maka dapat digambarkan heap tree sebagai berikut :

Akan tetapi pada metode heap sort, dibutuhkan heap tree dalam kondisi max-heap. Disini kita dapat melihat bahwa tidak semua parent node bernilai lebih besar dari child node (ini adalah sifat max-heap), maka kita perlu menyusun heap tree dalam kondisi max-heap. Maka kita membutuhkan dua metode heap sort, yaitu Build-Max-Heap dan Max-Heapify

Berikut ini adalah ilustrasi dari penggunaan metode HeapSort, Build-Max-Heap, dan Max-Heapify dalam sebuah heap tree :

HeapSort(A)

1. Deklarasi array A
2. Deklarasi elemen
3. Input elemen array A
4. Input nilai-nilai elemen array A
5. Build-Max-Heap
6. for (i = elemen-1 ; i >0)
7. Tukar A[i] dengan A[0]
8. Elemen-1
9. Max-Heapify(A, 1) 
10. End for

Dapat dilihat bahwa fungsi HeapSort akan memanggil dua fungsi yaitu Build-Max-Heap dan Max-Heapify, algoritma dari Build-Max-Heap adalah :

Build-Max-Heap(A)

1. for(i = (elemen-1)/2 ; i>=0)
2. Max-Heapify(A,i)
3. End for

Pada metode Build-Max-Heap terdapat for looping yang membagi dua jumlah elemen, disini elemen-1 karena pada array index awal adalah 0, sedangkan pada heap tree adalah 1, lalu elemen dibagi menjadi 2 dan selama i>= 0 maka for looping akan terus berjalan dan berikut ini adalah metode Max-Heapify :

Max-Heapify(A,i)

1. Deklarasi left = (i+1)*2 - 1
2. Deklarasi right = (i+1)*2
3. Deklarasi largest
4. if(left < elemen dan A[left] > A[i])
5. largest = left
6. end if
7. else
8. largest = i
9. end else
10. if(right < elemen dan A[right] > A[i])
11. largest = right
12. end if
13. if(largest != i)
14. Tukar A[i] dengan A[largest]
15. Max-Heapify(A,i)
16. end if

Misalkan ini adalah heap tree awal :

Karena pada heap tree jumlah node atau elemen ada 10 (dimana array ada 9), maka jumlah elemen dibagi 2 (10/2 = 5 dan 9/2 = 4) maka yang menjadi variabel i adalah 5 (untuk heap tree) atau 4 (untuk array) maka ilustrasinya adalah sebagai berikut :



Karena node parent sudah bernilai lebih besar dari child nodenya (16 > 7), maka pengecekkan berlanjut ke index berikutnya.




Disini, ternyata nilai yang dimiliki oleh index 4 bernilai lebih kecil dari kedua childrennya. Dalam kasus ini, akan ada penukaran elemen dengan perubahan sebagai berikut:





Selanjutnya adalah node 3 (index 3)

Disini node 3 bernilai lebih kecil dibandingkan kedua childrennya (9 dan 10). Maka akan terjadi penukaran dan perubahan sebagai berikut:

Selanjutnya kita akan mengamatii node 1 (index 2)

Disini ternyata node 1 bernilai lebih kecil dari kedua childrennya (14 dan 16), maka akan terjadi penukaran dengan children terbesarnya (hal ini karena setiap parent harus mempunyai nilai yang lebih besar dari childrennya) dan akan terlihat seperti gambar berikut :



Selanjutnya, kita beralih ke index 1 (root):



Disini kita melihat bahwa node 4 lebih kecil kedua childrennya (16 dan 10). Maka akan terjadi penukaran antara node 4 dengan node children max (16) seperti dibawah ini:



Disini kita akan mengecek kembali ke index 2 karena adanya perubahan yang ada dimana node 4 masih bernilai lebih kecil dari kedua childrennya (14 dan 7) dan akan mengalami perubahan sebagai berikut :



Dalam kasus ini, kita tidak mengecek index 3 karena parent (10) sudah bernilai lebih besar dari kedua childrennya (9 dan 3). Kita akan mengecek ke index 4, dimana node parentnya (4) masih mengalami violation karena bernilai lebih kecil dari childrennya (8). Disini akan terjadi penukaran dengan hasil seperti berikut :

Sampai langkah ini, proses Build-Max-Heap telah selesai karena masing-masing parent node sudah bernilai lebih besar dari child node dengan heap tree akhir sebagai berikut :



Setelah menggunakan metode Build-Max-Heap telah selesai, baru kita dapat menggunakan metode HeapSort untuk mengurutkan nilai pada array A. Setelah proses Build-Max-Heap, nilai pada index terakhir i akan ditukar dengan node 1 atau root selaam i > 0. Nilai 16 akan ditukar dengan nilai 1 dan jumlah elemen akan dikurangi 1. Namun, hal ini akan menyebabkan violation karena tidak memenuhi kondisi Max-Heap maka algoritma Max-Heapify akan dijalankan dengan ilustrasi sebagai berikut :



Sampai pada tahap ini, nilai tertinggi sudah berada di index yang benar (index terakhir 10 pada heap tree dan 9 di array). Langkah selanjutnya adalah mengulang langkah yang sama dengan for looping selama i > 0. Berikut ini adalah ilustrasi lengkapnya :

Maka, setelah algoritma HeapSort dilakukan, nilai-nilai pada array akan terurut dari nilai terkecil sampai nilai terbesar. A = 1, 2, 3, 4, 7, 8, 9, 10, 14, 16. Dan berikut adalah flowchat untuk algoritma HeapSort

Heap for Priority Queue

• Heap adalah implementasi dari priority queue sebuah data structure

• find-min : menemukan elemen terkecil dalam heap
• insert : memasukkan elemen baru ke dalam heap
• delete-min : menghapus elemen terkecil dari dalam heap

delete-min disebut pop, dan insert disebut push

Array Implementation

• Heap biasanya sudah diimplementasikan dalam array
• Elemen secara berurutan disimpan dari index 1 sampai N, dari atas ke bawah, dan dari node kiri ke node kanan dalam sebuah tree
• Root disimpan dalam index 1 (kita misalkan index 0 kosong untuk tujuan keamanan)
• Setiap node memiliki hubungan dengan parent, left child, dan right child untuk mempermudah pengecekkan
• Misalkan node yang sedang kita cek ber-index x.
• Parent(x) = x/2
• Left-child(x) = 2*x
• Right-child(x) = 2*x + 1

Inilah mengapa kita perlu menggunakan index 1 sebagai root, karena jika menggunakan index 0, index untuk parent, left-child, right-child akan berada di tempat yang sama yaitu, 0

Find-Min in Min-Heap

• Find-Min dalam Min-Heap cukup mudah
• Min-Heap pasti terletak di root, maka
• int findmin() {return data[1];}

Insertion in Min-Heap

• Ketika kita ingin memasukkan elemen baru dalam heap, kita harus tetap memperhatikan sifat-sifat heap
• Memasukkan setiap elemen baru di akhir heap (setelah index dari elemen terakhir)
• Upheap elemen baru (Menyesuaikan dengan sifat-sifat heap) 

Upheap in Min-Heap

• Membandingkan current node dengan parent node. Jika current node bernilai lebih kecil dari parent node maka kita harus melakukan tukar value dan melanjutkan UpHeap 
• Proses dihentikan jika parent node lebih kecil dari current node atau current node merupakan root (tidak punya parent)

Example of Insertion in Min-Heap

insert new node (20)

insert new node (5)

Deletion in Min-Heap

• Deletion dilakukan terhadap elemen terkecil yang terletak di root
• Mengganti posisi root dengan elemen terakhir dalam heap
• Mengurangi jumlah elemen dalam heap
• DownHeap root (Menyesuaikan dengan sifat-sifat heap)

DownHeap in Min-Heap

• Membandingkan current node (dimulai dari root) dengan left child dan right child. Apabila current node bernilai lebih besar dari child, maka lakukanlah penukaran value dan lanjutkan proses pada (child) node
• Proses dihentikan apabila current node sudah bernilai lebih kecil dari kedua children-nya atau current node merupakan leaf (tidak punya child)

Example Deletion in Min-Heap

Delete node(7)

Ganti root dengan elemen terakhir, node(28)

Cari posisi node (28) sesuai dengan sifat Min-Heap

Heap Complexity

• find-min       : O(1)
• insert            : O(log(n))
• delete-min    : O(log(n))

Max-Heap

• Setiap elemen node bernilai lebih besar dari child node
• Elemen terbesar terletak di root
• Max-Heap memiliki konsep yang sama dengan min-heap dimana bisa digunakan untuk membuat priotity queue dengan mencari elemen yang terbesar, dimana min-heap mencari elemen terkecil

Min-Max Heap

• Kondisi heap secara bergantian menunjukkan minimum dan maximum dari setiap level.
• Setiap elemen di level ganjil bernilai lebih kecil dari children di level ganjil
• Setiap elemen di level genap bernilai lebih besar dari children di level genap
• Tujuan dari min-max heap adalah mempermudah kita dalam menemukan kedua elemen, baik elemen terbesar maupun elemen terkecil dalam heap di waktu yang bersamaan.

Di dalam Min-Max Heap :

• Elemen terkecil terletak di root
• Elemen terbesar terletak di salah satu child dari root (left child atau right child)
• Elemen terbesar bisa terletak di root jika hanya ada satu elemen di dalam heap

findmin() {return data[1]; }

findmax() {return max(data[2], data[3]; }

Insertion in Min-Max Heap

• Elemen baru dimasukkan di akhir heap (setelah index dari elemen terakhir)
• Upheap elemen baru
• Upheap di dalam max-min heap berbeda dengan Upheap dalam min-heap ataupun max-heap

Upheap in Min-Max Heap

• Jika new node terletak di min-level
• jika parent new node bernilai lebih kecil dari new node, maka terjadi penukaran nilai dan upheapmax dari parent new node
• selain itu, upheapmin dari new node

• Jika new node terletak di max-level
• Jika parent new node bernilai lebih besar dari new node, maka terjadi penukaran nilai  dan upheapmin dari parent new niode
• selain itu, upheapmax dari new node

Upheapmin and Upheapmax in Max-Min Heap

• Upheapmin
• Membandingkan current node dengan grand-parent node. Apabila current node bernilai lebih kecil dari parent node, maka tukar dan rekursif upheapmin dengan grand-parent node.

• Upheapmax
• Membandingkan current node dengan grand-parent node. Apabila current node bernilai lebih kecil dari parent node, maka tukar dan rekursif upheapmin dengan grand-parent node.

Insert 50

• Upheapmin : 50 lebih besar dari parent node (28), maka upheapmax.
• Upheapmax : 50 lebih besar dari grand-parent node (35), maka tukar nilai keduanya.

• Upheapmax : karena node 50 tidak memiliki grand-parent, maka proses selesai

Insert 5

Upheapmin : 5 bernilai lebih kecil dari parent (14), maka tukar nilai dan rekursif upheapmin

Upheapmin : 5 bernilai lebih kecil dari grand-parent (8), maka tukar nilai dan rekursif upheapmin

Upheapmin : karena 5 tidak memiliki grand-parent, maka proses dihentikan

Deletion in Min-Max Heap

• Deletion of the smallest element
• Ganti root dengan elemen terakhir dalam heap
• Kurangi jumlah elemen dalam heap
• Downheapmin dari root

• Deletion of the largest element
• Ganti left child atau right child dari root (elemen terbesar) dengan elemen terakhir dalam heap
• Kurangi jumlah elemen dalam heap
• Downheapmax dari root

Downheapmin/max in Max-Min Heap

• Downheapmin
• Misalkan m adalah elemen terkecil dari current node children dan grandchildren 

• Jika m adalah grandchildren dari current node maka
• Jika m bernilai lebih kecil
• Tukar nilai
• Jika m lebih besar dari parent maka tukar nilai
• Rekursif downheapmin dari m

• Jika m adalah children dari current node
• Jika m lebih kecil dari current node
• Tukar nilai

• Downheapmax memiliki konsep yang sama dengan operator relasi yang dibalik

Min-Max Heap Delete Max

• Ganti nilai maksimum (50) dengan last node (14)

• Downheapmax : cari elemen terbesar dari children dan grandchildren. Setelah itu, tukar nilai keduanya

• Karena parent dari 14 bernilai lebih besar, maka tukar nilai keduanya, dan rekursif downheapmax

• Karena 28 tidak memiliki children ataupun grandchildren, maka proses selesai

Tries

• adalah suatu tree yang tersusun dalam data structure dengan menggunakan array (string)
• tries dapat menemukan satu kata di dalam kamus hanya dengan prefix dari sebuah kata

Property

• tries adalah tree dimana setiap vertex menggambarkan satu kata atau prefix
• root disimbolkan sebagai karakter kosong ('')
• vertex yang memiliki k sisi dari root memiliki prefix dengan panjang k
• jika a dan b adalah vertices dari sebuah tries dan kita mengasumsikan bahwa a adalah direct parent dari b, maka b adalah prefix asosiasi dari a

Example

Misalkan terdapat tries yang memuat kata-kata berikut :

1. Algo
2. Api
3. Bom
4. Bos
5. Bosan
6. Bor

kita bisa mengimplementasikan tries dengan structure berikut :

struct trie {  char chr;  int  word;  struct trie* edge[128];} *root = 0;•root = (struct trie*)malloc(sizeof(struct trie));root->chr  = ‘’;root->word = 0;

chr adalah karakter yang disimpan di dalam node

word akan bernilai 1 jika ada kata yang berada di akhir node, selain itu nilai word 0

Insertion in Tries

Untuk memasukkan word ke dalam tries, kita dapat menggunakan code berikut :

main function

char s[100];

insert(root, s);

void insert(struct trie *curr, char *p) {

  if ( curr->edge[*p] == 0 )

  curr->edge[*p] = newnode(*p);

  if ( *p == 0 ) curr->word = 1;
  else insert(curr->edge[*p],p+1);

}

newnode() function

struct trie* newnode(char x) {

  struct trie* node =

  (struct trie*)malloc(sizeof(struct trie));

  node->chr  = x;

  node->word = 0;

  for (i = 0; i < 128; i++ )

  node->edge[i] = 0;

  return node;

}

Finding in Tries using Prefix

misalkan kita ingin menemukan semua string yang mungkin dengan prefix yang ada :

pertama, kita harus meletakkan lokasi karakter terakhir (s/prefix) di dalam tries :

char s[100] = {“...”}; // global

•

int  i, n, okay;

struct trie *curr;

n    = strlen(s);

okay = 1;

curr = root;

for ( i = 0; i < n && okay == 1; i++ )

  if ( curr->edge[s[i]] == 0 ) okay = 0;

  else curr = curr->edge[s[i]];

if ( okay ) find(curr,n);

dan find function (akan mencetak semua kemungkinan strings yang memiliki prefix)

void find(struct trie *curr, int x) {

  if ( curr->word == 1 ) {

  s[x] = 0;

  puts( s );

  }

  for ( i = 0; i < 128; i++ )

  if ( curr->edge[i] != 0 ) {

  s[x] = i;

  find(curr->edge[i],x+1);

  }

}