AVL Tree

AVL Tree adalah Binary Tree yang sudah dapat melakukan self-balancing terhadap node di dalam tree-nya





Dalam AVL Tree, terdapat 3 komponen utama yaitu:

1. Key / Data yang bersifat unik
2. Level ( perhitungan dari root sampai node / leaf terjauh )
3. Balance Factor ( perbedaan level dari anak kiri dan anak kanan )

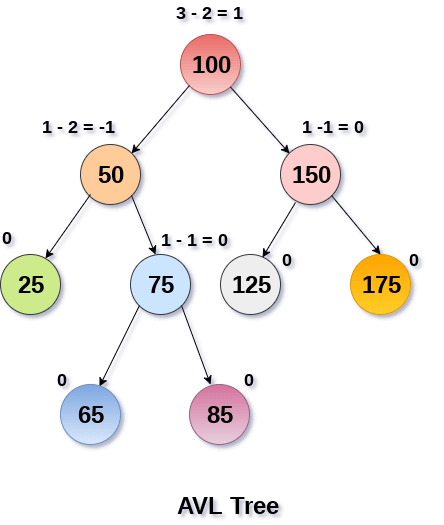
Dalam Gambar, yang diberi warna biru muda memiliki:

1. Key = 75
2. Level = 3 ( dihitung dari key 100, key 50, dan key 75 )
3. Balance Factor = 0, yang dilihat dari level anak kiri 75 yaitu, 65 dan anak kanan 75 yaitu, 85, maka 1-1 = 0

Balance Factor dapat dilihat sebagai berikut : 

• Leaves selalu memiliki balance factor 0 dan level 1 karena leaves adalah node terujung dan tidak memiliki anak 
• Dari leaves ke induknya, maka balance factor dan level dihitung dengan ketentuan: 
• Level Induk = [Level tertinggi anak] + 1
• Balance Factor = [Level anak kiri] - [Level anak kanan]
• Sebuah node tidak boleh memiliki Balance Factor lebih dari 1. Jika terdapat node yang memiliki node lebih dari 1, maka dianggap terjadi violation di dalam node tersebut. 

Insertion

Secara umum, Insertion di dalam AVL Tree sama dengan BST yaitu node dengan key yang lebih kecil akan disimpan di sebelah kiri, dan node dengan key yang lebih besar akan disimpan di sebelah kanan induknya.

Dalam gambar diperhatikan node 75 ada di sebelah kanan node 50 karena node 75 bernilai lebih besar dibandingkan node induk 50, sedangkan node 65 ada di sebelah kiri node 75 karena node 65 bernilai lebih kecil dibandingkan node induk 75.

Karena ini adalah Balanced Binary Search Tree, maka perbedaan muncul setelah insert dilakukan. Dalam AVL Tree, terdapat self-balancing yang dilakukan dengan cara mencari node yang terkena Violation

Violation dalam AVL Tree terjadi ketika sebuah node memiliki Balance Factor lebih dari 1 

Dalam Original AVL Tree, jika angka 4 diinsert, maka node 3 akan mengalami violation. Hal ini dikarenakan node akan memiliki level dan balance factor sebagai berikut :

Pada Original AVL Tree :

1.     Node 5, 9, dan 15 memiliki level 1 dan balance factor 0, hal ini karena node tersebut adalah leaf / terletak di ujung

2.       Node 14 adalah induk node 9 dan node 18, maka level node 14 adalah 3 ( dihitung level 1 dari node 14) dengan balance factor ( 1 – 2 ) = -1. Dan begitu seterusnya.

3.       Dalam simulasi point minus (-) diabaikan tetapi di dalam kode digunakan karena minus  hanya menandakan tidak seimbang ke kiri dan plus tidak seimbang ke kanan

Kita harus mempunyai persepsi bahwa :

1.       Node 4 (Child), node yang diinsert

2.       Node 5 (Parent), adalah induk dari node yang diinsert

3.       Node 3 (Grand Parent), adalah Induk dari Induk node yang diinsert

Jika node 4 di insert, maka akan terlihat seperti gambar di bawah ini :

1.       Node 4 akan masuk di sebealh kiri node 7 dan menjadi anak kiri node 5 karena node 4 memiliki key yang lebih kecil dari node 7, lebih besar dari node 3 dan lebih kecil dari node 5

2.       Setelah sampai pada posisinya, maka akan dihitung level dan balance factor dari node yang baru di insert (node 4).

Dimana :

o   Node 4 akan diberikan 1,0 karena merupakan node leaves

o   Lalu, penghitungan akan berlanjut ke induk dari node 4 yaitu 5, dengan level 2 (node itu sendiri + 1 tingkat dibawahnya) dan balance factor 1 (anak kiri = 1 (node 4) dan anak kanan = 0)

o   Penghitungan untuk induk node 5, yaitu node 3 dengan level 3 (nodenya sendiri + ada dua tingkat dibawahnya) dan balance factor 2 ( jarak terpanjang ke node leaves ), maka disini terjadi violation

Lalu, kita harus mengidentifikasi jenis Violation yang terjadi, terlebih dahulu ada empat jenis violation yang dapat terjadi :

1. Left-left case, dimana Child adalah anak kiri Parent dan Parent adalah anak kiri Grand-Parent
   
2. Right-right case, dimana Child adalah anak kanan Parent dan Parent adalah anak kanan Grand-Parent
   
3. Left-right case, dimana Child adalah anak kanan Parent dan Parent adalah anak kiri Grand Parent
   
4. Right-left case, dimana Child adalah anak kiri Parent dan Parent adalah anak kanan Grand-Parent
   

Note : H+1 menandakan adanya perubahan height (level) karena adanya penambahan node baru

Jika terjadi violation maka akan dilakukan solving/rebalancing dengan cara berikut :

1)      Jika menemukan case 1 atau case 2, maka akan dilakukan single rotation

2)      Jika menemukan case 3 atau case 4, maka akan dilakukan double rotation

Single Rotation

Terdapat dua jenis Single Rotation yaitu :

1. Left-left rotation untuk menyelesaikan case 1
2. Right-right rotation untuk menyelesaikan case 2

a.      Perhatikan bahwa S adalah induk dari SubTree A, sehingga S adalah Parent dan T adalah Grand Parent.

Note : Subtree A adalah subtree yang didalamanya terdapat node yang baru diinsert

b.      Left-left rotation dilakukan dengan putaran ke kanan dengan S berperan sebagai poros.

c.      T (Grand Parent) akan turun menjadi Right Child dari S.

d.      Subtree A akan berposisi sejajar dengan T sebagai Parent dengan status sebagai Left Child dari S.

e.      Perhatikan bahwa sebelumnya S memiliki Right Child yaitu SubTree B, sedangkan T memiliki Right Child yaitu SubTree C. Setelah left-left rotation, maka SubTree B secara otomatis akan menjadi Left Child T dan SubTree C akan tetap menjadi Right Child dari T.

f.    Kita tidak perlu mengetahui apa yang ada di dalam SubTree A,B, dan C karena yang perlu dilihat adalah pivot S,T, dan Induk dari SubTree A ( terdapat node yang baru diinsert )

Maksud dari point f, apabila node yang baru diinsert adalah node 12 (seperti gambar di samping), maka yang terlihat adalah :

1.       Node 22 berperan sebagai pivot S.

2.       Node 30 berperan sebagai pivot T, Grand Parent yang akan turun menjadi Right Child dari S.

3.       Node 15 akan berperan sebagai induk dari SubTree A ( karena mengandung node yang baru diinsert, yaitu 12 )

4.       Node 27 akan berperan sebagai induk dari SubTree B

5.       Node 45 akan berperan sebagai induk dari SubTree C

a.       S adalah Induk dari SubTree A, sehingga S adalah Parent, dan T adalah Grand Parent.

Note: Subtree A adalah sebuah subtree yang didalamnya diinsert node baru.

b.       RR Rotation dilakukan dengan melakuan putaran ke arah kiri, dengan poros S.

c.       T (Grand Parent) akan turun menjadi Left Child dari S.

d.       SubTree A naik ke tempat parent dengan mempertahankan status sebagai anak kanan S.

e.       anak kiri dari S (SubTree B) akan menjadi anak kanan dari T. Sehingga T akan memiliki anak kiri SubTree C dan anak kanan Subtree B.

f.        Kita tidak perlu mengetahui apa yang ada di dalam SubTree A,B, dan C karena yang perlu dilihat adalah pivot S,T, dan Induk dari SubTree A (terdapat node yang baru diinsert)

Double Rotation

Adalah rotasi dengan menggunakan dua metode single rotation. Jenis rotasi ini dilakukan untuk menyelesaikan case 3 dan case 4

a)       Penyelesaian dimulai dari Parent (Node S) yang akan mengakibatkan First Rotation

Untuk case 3 ini, kita diharapkan melihat child dari pivot R, yaitu anak kiri (SubTree B1) dan anak kanan (SubTree B2)

Hal yang perlu diperhatikan :

1.       Node S adalah Grand Parent

2.       Node R adalah Parent

3.       Pilih Subtree yang akan diamati.

(Dalam hal ini kita akan memilih B2 agar tidak menjadi double rotation lagi)

4.       Lakukan RR Rotation

Hasil First Rotation :

b)       Lalu, selesaikan case dari Grand Parent (node T) dan lakukan Second Rotation

Dari hasil first rotation, dapat dilihat bahwa case mirip dengan case 1, yaitu left-left case, maka akan dilakukan rotasi ke kanan dan mendapatkan hasil sebagai berikut :

Perhatikan bahwa parent R akan menjadi induk dari child S dan Grand Parent T. Hal ini akan membuat tree menjadi seimbang karena SubTree B2 yang awalnya menjadi Right Child dari R berpindah menjadi Left Child dari pivot T.

Deletion

Dalam melakukan delete node, kita harus meng-update balance factor dari masing-masing node 

untuk mengetahui apakah akan terjadi violation setelah delete.

Ketika kita melakukan deletion pada node 5, bisa dipastikan bahwa akan terjadi violation pada node 10 karena node 10 akan memiliki balance factor -2 (tidak seimbang ke kiri)

Perbaikan setelah violation seperti gambar di bawah : 

Cara mendeteksi violation adalah dengan melihat balace factor dari node dan childnya. Apabila balance factor minus, berarti kita harus cek ke bagian kanan (tidak seimbang ke kiri) dan sebaliknya. Jika seimbang, boleh pilih salah satu.